

المحايد/ منوعات
فهم البابليون القدماء المفاهيم الأساسية في الهندسة، بما في ذلك كيفية عمل مثلثات قائمة الزاوية بدقة، إذ استخدموا هذه المعرفة الرياضية لتقسيم الأراضي الزراعية منذ زمن بعيد.
وكشفت دراسة حديثة نُشرت في مجلة "فاونديشنز أوف ساينس" أن البابليين القدماء فهموا نظرية فيثاغورس قبل أكثر من ألف عام من ولادة الفيلسوف اليوناني فيثاغورس، الذي يعرف على نطاق واسع بأنه ببأنه لد أول من نظر لهذه الأفكار.
ويقول الباحث الرئيسي دانيال مانسفيلد من كلية الرياضيات والإحصاء بجامعة نيو ساوث ويلز في سيدني بأستراليا: "إن البالبليين استخدموا الفهم النظري للأشياء للقيام بأشياء عملية، ومن الغريب جدًا رؤية هذه الأشياء منذ 4000 عام تقريبًا".
وكانت بابل واحدة من عدة مجتمعات قديمة متداخلة في بلاد ما بين النهرين، وهي منطقة في جنوب غرب آسيا كانت تقع بين نهري دجلة والفرات فيما يعرف اليوم بدولة العراق.
ووُجدت حضارة بابل في الفترة ما بين 2500 و500 قبل الميلاد، وسيطرت الإمبراطورية البابلية الأولى على مساحة كبيرة بين عامي 1900 و1600 قبل الميلاد.
لوح بليمبتون 322
وكان مانسفيلد يدرس قرصا طينيا مكسورا من هذه الفترة، يُعرف باسم بليمبتون 322، وهو مغطى بعلامات مسمارية تشكل جدولا رياضيا يسرد "ثلاثيات فيثاغورس".
وكل ثلاثية هي أطوال الأضلاع الثلاثة لمثلث قائم الزاوية، حيث يمثل كل ضلع عددا صحيحا؛ أبسط مثال هو (3، 4، 5) ؛ تشمل الأخرى (5، 12، 13) و(8، 15، 17).
وأضلاع المثلثات هي هذه الأطوال لأنها تخضع لنظرية فيثاغورس: مربع الضلع الأطول يساوي مجموع مربعي الضلعين الآخرين. تم تسمية هذا الجزء الكلاسيكي من الرياضيات على اسم الفيلسوف اليوناني فيثاغورس، الذي عاش بين حوالي 570 و 495 قبل الميلاد - بعد وقت طويل من صنع لوحة بليمبتون 322.
ويقول مانسفيلد: "لقد عرف البابليون الأوائل نظرية فيثاغورس.. لكن يبقى السؤال الكبير هو لماذا استعان بها البابليون؟"
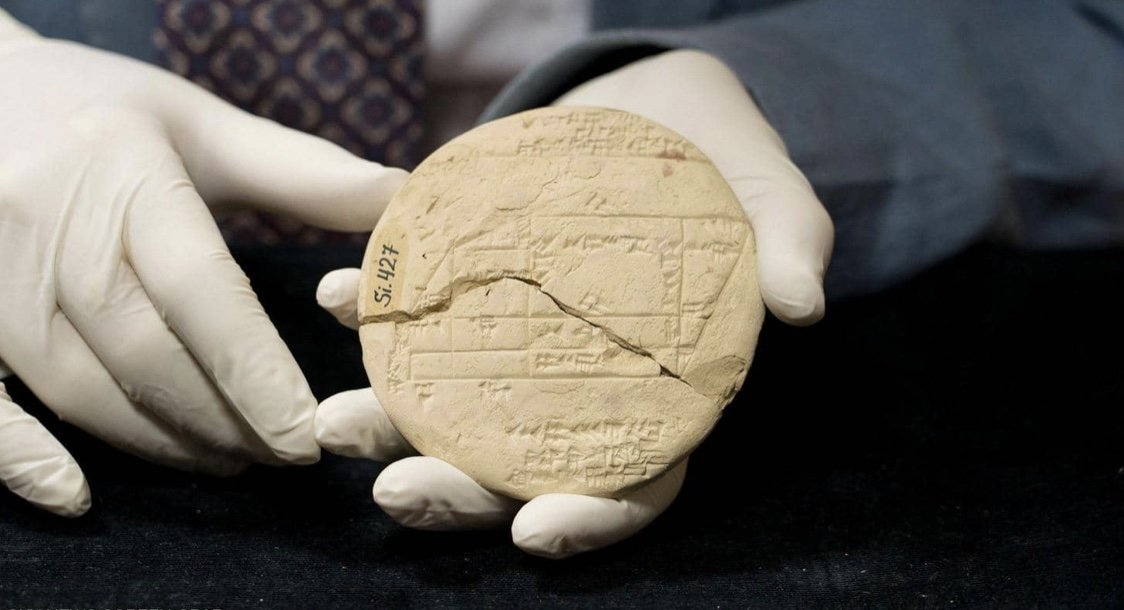
ويعتقد مانسفيلد أنه وجد الجواب أخيرا، حيث كان المفتاح الرئيسي للإجابة هو اللوح الطيني الثاني، المسمى Si.427، الذي تم التنقيب عنه في العراق عام 1894 بواسطة بعثة آثار فرنسية، وتتبعه مانسفيلد ووصل إليه حيث يُحفظ في إسطنبول.
ويعتقد مانسفيلد إن لوح Si.427 يعود إلى ما قبل تاريخ بليمبتون 322 وربما يكون مصدر إلهام له.
وكان Si.427 عبارة عن لوحة مساح يستخدم لإجراء الحسابات اللازمة لتقاسم قطعة أرض بشكل عادل عن طريق تقسيمها إلى مستطيلات.
ويقول مانسفيلد: "دائما ما تكون المستطيلات متزعزعة بعض الشيء لأنها تقريبية فقط". لكن Si.427 لوح مختلف، يقول: "المستطيلات مثالية"، حقق المساح ذلك باستخدام ثلاثيات فيثاغورس.
ويتابع مانسفيلد: "حتى أشكال هذه الأجهزة اللوحية تحكي قصة.. Si.427 عبارة عن لوح يدوي.. التقط شخص ما قطعة من الطين، ووضعها في يده وكتب عليها أثناء مسح أحد الحقول".
على الرغم من أن الأسباب الكامنة وراء حسابات حدود الأرض على اللوح ليست واضحة تماما، إلا أن لوح Si.427 يحكي قصة نزاع حول أشجار النخيل على الحدود بين ممتلكات شخص بارز يُدعى Sin-bel-apli ومالك أرض ثري.
في المقابل، قال مانسفيلد إن لوح بليمبتون 322 هو تحقيق منهجي لثلاثيات فيثاغورس، ربما مستوحى من الصعوبات التي واجهها المساحون، فهو يعود إلى فترة بدأت فيها الأرض تتحول إلى ملكية خاصة، عندما بدأ الناس يفكرون في الأرض من منظور" أرضي وأرضك"، راغبين في إنشاء حدود مناسبة لإقامة علاقات جوار إيجابية.
على الرغم من مرور 1000 عام بين إنشاء الألواح وولادة فيثاغورس من ساموس في 570 قبل الميلاد - مما أدى إلى إضفاء الطابع الرسمي على قاعدة فيثاغورس يتم تدريسها في المدرسة اليوم – إلا أن المختصين يعرفون منذ فترة طويلة أن الإغريق ورثوا تعاليم الرياضيات من المصريين، والمصريين بدورهم عرفوها من البابليين.
ومع ذلك، فإن ما أدهش مانسفيلد هو مستوى التطور النظري الذي تكشفه الألواح عن البابليين القدماء الذين عاشوا في مثل هذه المرحلة المبكرة من تاريخ البشرية.
وقال: "لم يتوقع أحد أن البابليين كانوا يستخدمون ثلاثيات فيثاغورس بهذه الطريقة". "إنها أقرب إلى الرياضيات البحتة، المستوحاة من المشاكل العملية في ذلك الوقت".